
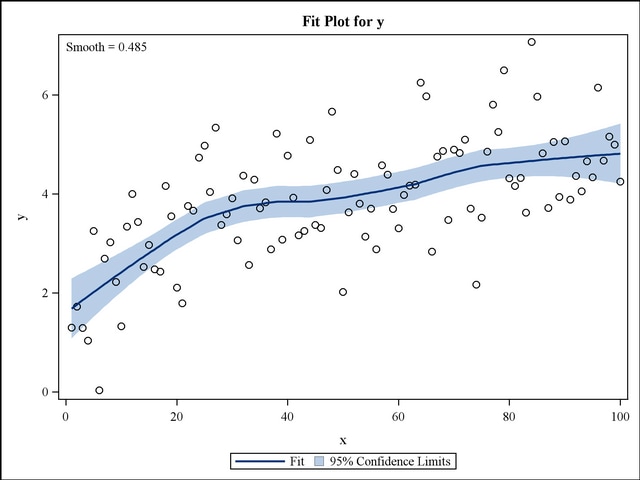
Plot(NF,ProEmig,main="Polynomial Model",xlab="NF",ylab="ProEmig") When I use the coefficients and make this equation ProEmig=1.470466- 0.870759NF+0.064054NF2 it does not fit into my data correctly. Variable lengths differ (found for 'NF2') X y<- predict(model5, list(NF=x),type="response")Įrror in (Terms, newdata, na.action = na.action, xlev = object$xlevels) : I looked at this example you provided in your page and I was wondering how you can plot curve on scatter plot when you have quadratic effect of the same variable (in my case NF2)?When i try to follow what you did for your example I keep getting the following error: What I read was to use the coefficients from the summary table of this model to make the line: I need to use this model to fit a curve to my scatter plot to show the quadratic effect of initial density on proportion emigrating. The productivity did not have any effect and I reached to the following final model: I have used glm with quasibinomial error to look at the effect of productivity and initial density on proportion of insect emigration. David holds a doctorate in applied statistics.Ĭoefficients in a polynomial glm with family binomial and fit a curve to scatter plot His company, Sigma Statistics and Research Limited, provides both on-line instruction and face-to-face workshops on R, and coding services in R. That wasn’t so hard! In our next article, we will look at other applications of the glm() function.Ībout the Author: David Lillis has taught R to many researchers and statisticians. As the predictor increases, the probability decreases. We can see that for both predictors, there is a negative relationship between the probability that vs=1 and the predictor variable. 71.1 472.0 xdisp ydisp plot(mtcars$disp, mtcars$vs, pch = 16, xlab = "DISPLACEMENT (cubic inches)", ylab = "VS") lines(xdisp, ydisp) Residual deviance: 22.696 on 30 degrees of freedomĪIC: 26.696 Number of Fisher Scoring iterations: 6 range(mtcars$disp) Joining such a large number of closely spaced points will give a smooth appearance to our model. So we create a sequence of values between 0 and 6 in increments of 0.01. range(mtcars$wt)Ī range of wt values between 0 and 6 would be ideal. This range of values we can establish from the actual range of values of wt. To plot our model we need a range of values of weight for which to produce fitted values. Residual deviance: 31.367 on 30 degrees of freedomĪIC: 35.367 Number of Fisher Scoring iterations: 5 codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 43.860 on 31 degrees of freedom Glm(formula = vs ~ wt, family = binomial, data = mtcars) Deviance Residuals: So first we fit a glm for only one of our predictors, wt. Now we want to plot our model, along with the observed data.Īlthough we ran a model with multiple predictors, it can help interpretation to plot the predicted probability that vs=1 against each predictor separately. We continue with the same glm on the mtcars data set (regressing the vs variable on the weight and engine displacement). This is 2.835 with(RegADHD, table(ADHD $Score, ADHD$Group))ĭoes this mean that the probability of having a higher score (in ADHD) increases 2.835 times with being in the severe exposure group, compared with no exposure? But then I don´t know anything about less exposure.In our last article, we learned about model fit in Generalized Linear Models on binary data using the glm() command. To get the odds I did: round(exp(RegADHD$beta), 3) More specifically, I struggle because I get only one value (for group 3). (2 observations deleted due to missingness)īut I don´t really understand what is the interpretation of this coefficient?

I am new to this and used this formula: RegADHD |z|) I have a question regarding the interpretation of an ordinal regression in R with the clm function.


 0 kommentar(er)
0 kommentar(er)
